Sampling large data sets (Part 2)

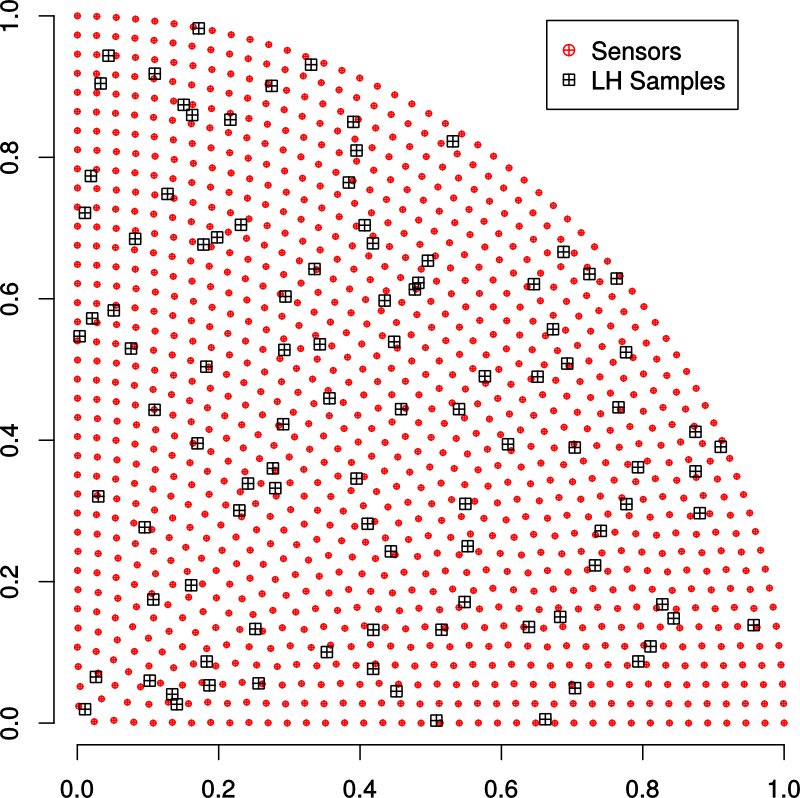
Recall that we had found a set of points that samples a cylindrical domain uniformly.
However, these points do not match the locations of our sensors and we will have to find the nearest sensor to each sample point.

This problem is a version of the Assignment Problem and an elegant way of proceeding is to use the Hungarian Algorithm. A clear description of the problem and the algorithm that is used to solve it can be found at http://www.math.harvard.edu/.

We have 50,000 sensors and 100 sample points. If we want to solve the assignment problem directly on our desktop, the memory requirement for the complete problem is around 23 Gb

• more than the free memory available in most desktops. So we have to simplify the problem to suit the resources that we have available.

The R package fields has a method rdist for computing the Euclidean distance matrix. We first find the pairwise distances between the sensors and the samples

  # Install and load the fields library
  install.packages("fields")
  library("fields")

  # Get the Euclidean distance matrix 
  # between the sensors and the samples
  # 50,000 sensors and 100 samples
  distances <- rdist(inputData, sampleData)

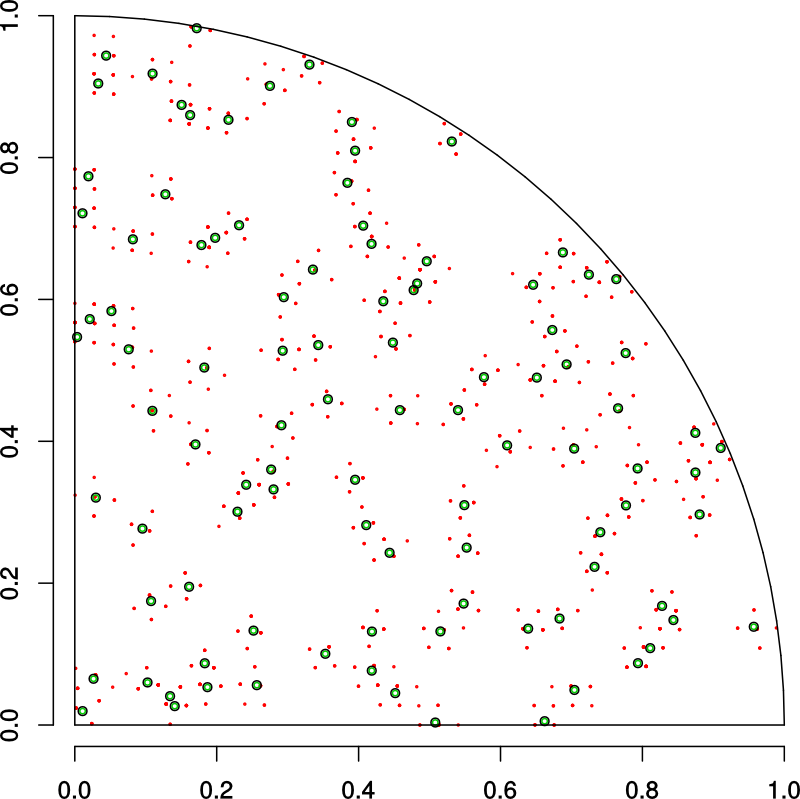
Next we define a radius of support around each sample location and find the sensors in that region.

  # Find a sparser matrix based on a radius of support
  supportRadius <- max(rdist(inputData[1:1],inputData[4:4]))
  distanceFlags <- ifelse(distances < supportRadius, 0, 1)
  sparseIndices <- which(distanceFlags == 0, arr.ind=T)
  sparseInputData <- inputData[sparseIndices[,1]]

This procedure gives us the sensor locations (in red) that we care about. Now we can recompute a much smaller distance matrix and apply the Hungarian algorithm to find which sensors are closest to our sample points.

The clue package in R provides us with the required tools to solve the Linear Sum Assignment Problem and the computation is direct:

# Find the distances between the input data and the sample data
distancesSparse <- rdist(sparseInputData, sampleData)

# Use Hungarian algorithm to minimize pairwise Euclidean norm
sol <- solve_LSAP(t(distancesSparse))

The sample sensors can now be identified from the output of the assignment algorithm and use in our training exercise.

If the training set is a large fraction of the total number of sensors (typically 80%-90%), the approach that we have used becomes inefficient and other sampling techniques may be preferred. We will talk about some of of these in the next part of this series.